teaching machines

CS 330 Lecture 32 – Taming Recursion

April 24, 2017 by Chris Johnson. Filed under cs330, lectures, spring 2017.

Dear students,

We’ve seen that Haskell does some pretty crazy things: it infers types, it supports this crazy pattern matching stuff, it disallows side effects, and it computes things lazily. Let’s look at one last crazy thing it does: it uses recursion for everything! There are no loop control structures.

Normally, when you think of recursion, what’s the first thing that comes to mind?

Performance is probably not what you’re thinking of. I think stack overflow exceptions. Why does recursion lead to stack overflow exceptions? Because every time you call a function, we throw onto the stack a new stack frame holding the function’s parameters, local variables, and

Today we’re going to look at two tricks that can make recursive algorithms have much better performance.

The first of these is called memoization. We define it as follows:

Memoization is the act of caching the result of a routine to speed up subsequent invocations of that routine.

We’ve already seen memoizing once. When we added lazy evaluation to Ruby using our Lazy class, we delayed the computation by putting it in a block, and then cached its result the first time it was executed. Today we’re going to use a similar idea to make repeated recursive function calls really speedy.

Let’s start off by visualizing a recursive algorithm. I really have no tolerance for several tired old programming problems: the Towers of Hanoi, Fahrenheit to Celsius conversion, the shape hierarchy, and the Fibonacci sequence. However, the familiarity of these problems is actually helpful today. Let’s look at a Fibonacci “tree” for the sixth Fibonacci number:

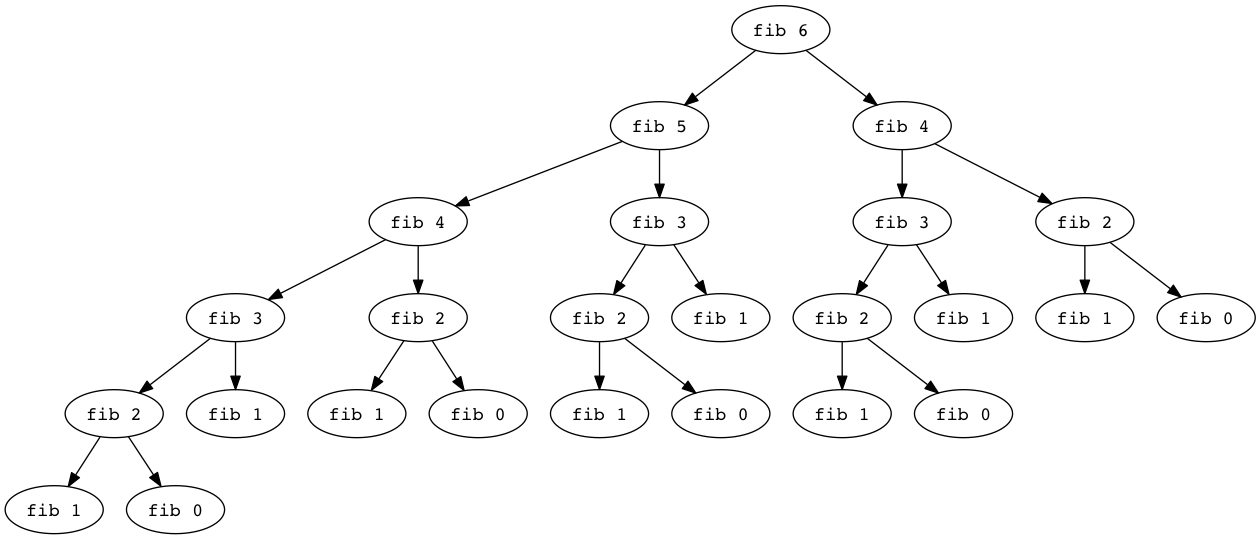
What do you notice? What happens when we compute the seventh Fibonacci number?

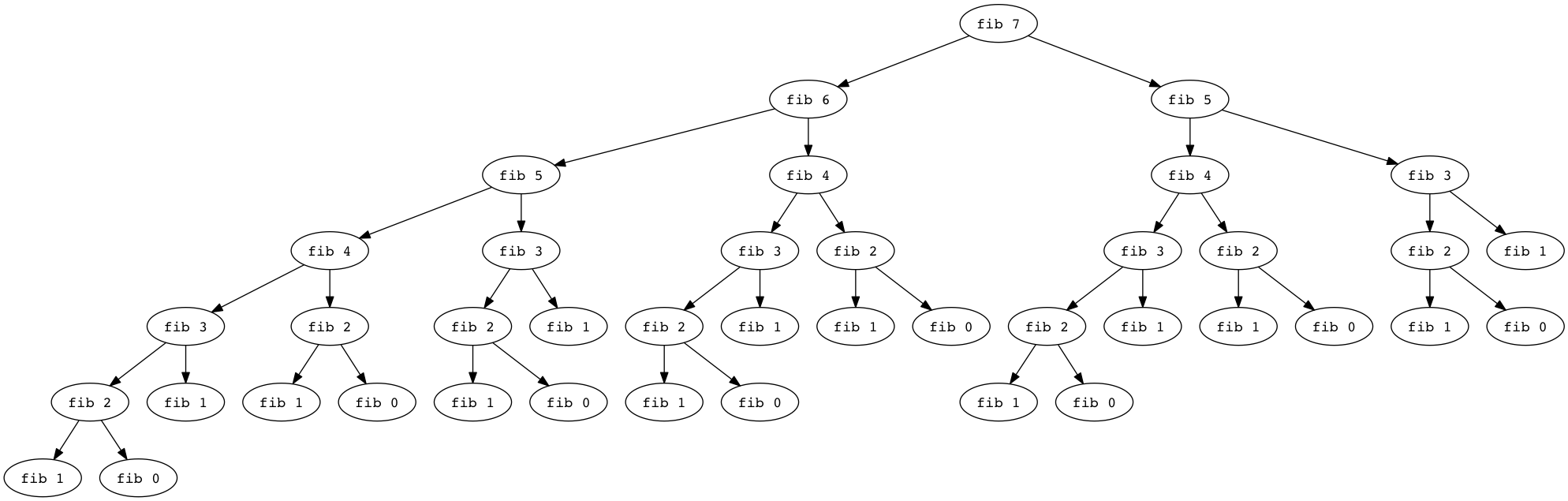
That’s a lot of duplicated calls, eh? Is that a big deal? Maybe not. Let’s try implementing it:

def fib n
  if n <= 1
    n
  else
    fib(n - 1) + fib(n - 2)
  end
end

n = ARGV[0].to_i
puts fib n

Let’s see how well this scales. We’ll try various values of n and see what happens.

We’ll find that all this duplication does indeed takes its toll. What if somehow we could cache the value of a “tree” and not have to recurse through it if we’d already done so? Let’s try. But how will we do this? How do we remember what the results are for a previous tree? Well, we can create a dictionary mapping the function’s parameter to its return value. Like this:

$cache = Hash.new

def fib n
  if $cache.has_key? n
    $cache[n]
  else
    value = fib(n - 1) + fib(n - 2)
    $cache[n] = value
  end
end

n = ARGV[0].to_i
puts fib n

This is a whole lot faster. How much work have we saved? Well, look at this tree for fib 6:

And for fib 7:

We have turned what was an algorithm of exponential complexity into one of linear complexity—assuming the cost of dictionary lookup is neglible.

That’s great, but having to explicitly add memoization to the function is kind of annoying. What we added had very little to do with the Fibonacci sequence. Hmm… Maybe we could write a higher-order function that automatically wrapped up a function inside a memoizing routine? Yes, we can. In fact, the technique we’ll use is called method wrapping. And we can also get rid of that nasty global cache.

It would be great if we could write something like this:

fib = memoize(fib)

That way we could continue to call fib like normal. Memoization would just be an implementation detail, as it should be.

Let’s solve this in steps. The memoizing function will need to accept another function as its parameter. We’re going to use Ruby symbols for this, which are kind of like method references in Java 8:

def memoize fid
  ...
end

fib = memoize(:fib)

Also, the arity of functions is going to be important here. For the time being, let’s say our function only works with functions of arity 1:

def memoize1 fid
  ...
end

fib = memoize(:fib)

Next, we’ll need a cache:

def memoize1 fid
  cache = Hash.new
  ...
end

Then let’s overwrite our function with a new one. We’ll use some Ruby magic for this:

def memoize1 fid
  cache = Hash.new

  define_method(fid) do |arg|
    # method body here
  end
end

Hang on. If we overwrite our function with this memoizing wrapper, we won’t be able to call the real one when we need it. Let’s retain a reference to the old one. Here’s a complete wrapper which adds absolutely no extra work around the function:

def memoize1 fid
  cache = Hash.new
  f = method(fid)

  define_method(fid) do |arg|
    f.call arg
  end
end

Let’s add the memoization work:

def memoize1 fid
  f = method(fid)
  cache = Hash.new

  define_method(fid) do |arg|
    if cache.has_key? arg
      cache[arg]
    else
      value = f.call arg
      cache[arg] = value
    end
  end
end

Closures to the rescue here! They saved us from our global cache. First-class functions to the rescue too! We stored the old function in a local variable that is also referenced by the closure.

For the curious, we can also generalize this code to work for functions of arbitrary arity using Ruby’s splat operator:

def memoize fid
  f = method(fid)
  cache = Hash.new

  define_method(fid) do |*args|
    if cache.has_key? args
      cache[args]
    else
      value = f.call *args
      cache[args] = value
    end
  end
end

Let’s try this out on a different recursive function, for a problem taken from the MICS 2017 programming contest. Suppose you are standing at an intersection of a city. You are trying to get to a certain other intersection. How many ways can you get there, assuming you never go out of your way?

Consider this example where you 3 blocks north and 2 blocks west of your destination. You could go DDRRR, DRDRR, DRRDR, DRRRD. Or RRDRD, RRRDD, RDDRR, RDRDR, RDRRD, or RRDDR. That’s ten different options.

Like most recursive problems, this feels really obtuse but has a simple solution:

def nroutes x, y
  if x == 0 && y == 0     # We've arrived!
    1
  elsif x < 0 || y < 0    # We're gone out of our way. Illegal.
    0
  else
    nroutes(x - 1, y) +   # How many paths if we right?
    nroutes(x, y - 1)     # How many paths if we down?
  end 
end

When we run this, it start to get bogged down very quickly. But there’s a lot of tree revisiting here, just as with Fibonacci. Let’s memoize:

memoize(:nroutes)

And it’s beautifully fast.

Okay, pruning out the recursive calls that you’ve already done before is one way to tame recursion. Let’s look at another. We mentioned early that the piling up of stack frames is what gets recursion in trouble. Consider this definition of sum' in Haskell:

sum' [] = 0
sum' (first:rest) = first + sum' rest

When we say sum' [1..5], this sort of thing stacks up in RAM:

No single instance of the function call can finish until we reach the base case. The general cases sit idly consuming memory. Well, what if we could make it such that the general cases had nothing left to do? What if we sent a general cases’ work along to the recursive call? We can do this by adding another parameter—called an accumulator because it accumulates up the results:

sum' accumulator [] = accumulator
sum' accumulator (first:rest) = sum' (first + accumulator) rest

The recursive call is said to be in the tail position of the function. It’s the very last thing left to do in the function’s body. With this arrangement, our call stack becomes this:

Notice that there’s no work left for the general cases to complete after the recursive call finishes. We might as well just reuse the current call’s stack frame instead of pushing on a new one. This reuse would make recursion cost no more than conventional iteration.

This practice of a compiler recognizing that a recursive call is the only remaining work for a function to do, and having the recursive call overtake the caller’s stack frame, is called tail call optimization. Not all compilers support it, but Clang, GCC, and GHC do under certain conditions. If you recursion is getting out of hand, try using an accumulator to get the recursive call into the tail position.

Here’s your TODO list:

• Start the WASD homework, which is due before May 15.

See you next time, when we discuss state machines and regular languages!

Sincerely,